| Definitions | x:A  B(x), P & Q, M1 || M2, Knd, Id, State(ds), Type, t.1, Top, f(x)?z, B(x), P & Q, M1 || M2, Knd, Id, State(ds), Type, t.1, Top, f(x)?z, 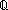 , t.2, Void, x:A , t.2, Void, x:A  B(x), <a, b>, f(x), f(a), IdDeq, f B(x), <a, b>, f(x), f(a), IdDeq, f 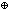 g, s = t, g, s = t,  x:A. B(x), t x:A. B(x), t  T, T,  b, b,  A, A,   b, b,  , ,  , ,  x.A(x), x.A(x),   x. t(x), KindDeq, a:A fp x. t(x), KindDeq, a:A fp B(a), product-deq(A;B;a;b), x B(a), product-deq(A;B;a;b), x  dom(f), P dom(f), P   Q, P Q, P    Q, Unit, left + right, Q, Unit, left + right, 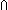 x:A.B(x), False, P x:A.B(x), False, P  Q, z != f(x) Q, z != f(x)   P(a;z), constant_function(f;A;B), M1 ||decl M2, Valtype(da;k), M.ds(x), mk-ma, MsgA, ma-ef-const(M;k;x;s;v), M.da(a), M.state, M1 P(a;z), constant_function(f;A;B), M1 ||decl M2, Valtype(da;k), M.ds(x), mk-ma, MsgA, ma-ef-const(M;k;x;s;v), M.da(a), M.state, M1 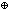 M2, Atom$n, f || g, if b then t else f fi , x,y:A//B(x;y), f M2, Atom$n, f || g, if b then t else f fi , x,y:A//B(x;y), f  g, True, g, True,  T, IdLnk, x(s), EqDecider(T), s ~ t, {T}, SQType(T), case b of inl(x) => s(x) | inr(y) => t(y), T, IdLnk, x(s), EqDecider(T), s ~ t, {T}, SQType(T), case b of inl(x) => s(x) | inr(y) => t(y),  , Dec(P) , Dec(P) |